Load Transfer Technology Based on Topology Operating State Identification
-
摘要:
针对变电站发生全停后开关状态无法识别而引发的问题,提出一种考虑配网实时运行方式的负荷转供技术。采用贝叶斯网络描述开关状态与节点电压的关系,识别配网的拓扑运行状态进而作为转供方案的基础。最后通过对某个实际配电系统的故障仿真分析,结果表明该方案可以有效提高停电负荷的转供能力。
Abstract:Aims at the problem that the switch state cannot be identified after the complete shutdown of the substation, this paper proposes taking into account the frequent topology changes. Bayesian networks are used to describe the relationship between switch status and node voltage, identify the topology of the distribution network, and serve as the basis for the power transfer scheme; Finally, through fault simulation analysis of an actual distribution system, result can effectively increase the transfer capacity of power outage load.
-
0. 引言
变电站全停事故是影响电网可靠运行的重要因素[1-2]。当变电站发生全停事故后,会直接引起地区大范围停电,造成巨大的经济损失。变电站全停所引起的馈线间的负荷转供实际上是大规模、非线性以及混合整型的优化问题。文献[3]提出以主变之间的联络线作为恢复路径,完成变电站之间的负荷转供。文献[4]考虑以主变间的互联关系作为转供条件,建立负荷转供模型,将全停主变的负荷均分配给具有联络关系的其他变电站 。
自负荷转供提出以来,都是在假设原始配电网拓扑运行状态是已知的前提下,很少讨论拓扑运行状态未知时如何进行负荷转供。本文提出了一种判断变电站全停时配网拓扑运行状态辨识的技术。首先,基于贝叶斯网络来建立开关状态和馈线上的电压数据之间的数学模型;接着在该模型上引入信念传播算法来辨识所有开关的状态,从而获得配电网的实际运行状态。在基于精确的拓扑运行状态下,生成最大恢复供电能力的负荷转供模型,从而提高整体负荷的最大恢复供电能力。
1. 基于贝叶斯网络的拓扑运行状态辨识
1.1 配网运行状态辨识模型
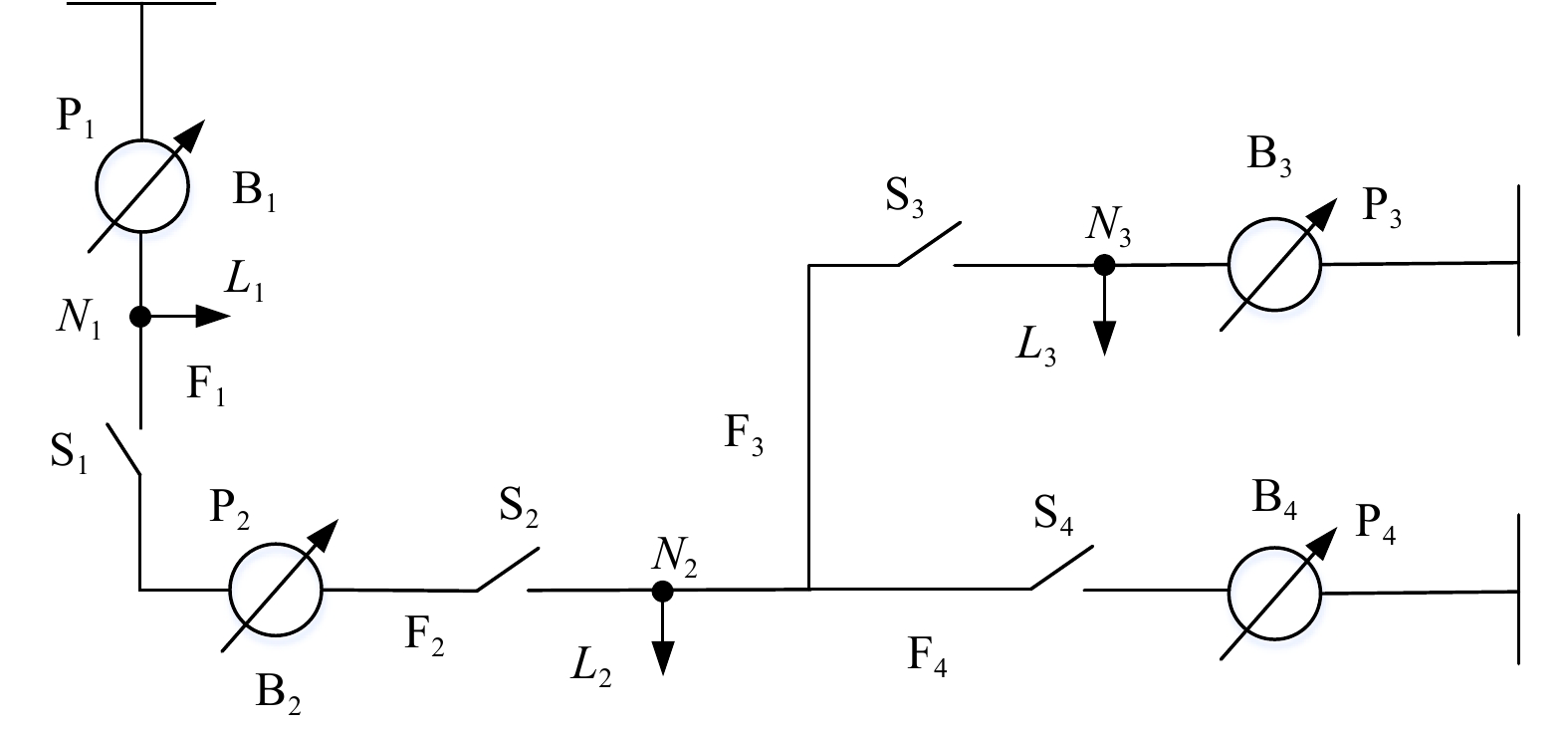
典型的配电网络结构包括变电站、母线、支路、馈线、变压器、开关、继电保护装置以及一些自动化设备。网络中开关的运行状态会因不定期变动,进而改变配电网的拓扑运行方式。 对典型的配电网结构进行简化,如图1所示为某一简化的配电网络,P1、P2、P3、P4为4所变电站的母线,而B1、B2、B3、B4为相应母线所连接的变电站,N1、N2、N3分别为网络中的等效负荷节点,L1、L2、L3表示其上相应的负荷,S1、S2、S3、S4表示网络中的开关,F1、F2、F3、F4分别表示节点之间的馈线。
皮尔逊相关系数是用来衡量数据间相关程度的评价指标,它以2组数据与各自平均值的离差为基础,通过2个离差相乘来反映2变量之间的相关程度,皮尔逊相关系数的定义为:
K=m∑i=1(Xi−ˉX)(Yi−ˉY)√m∑i=1(Xi−ˉX)2√m∑i=1(Yi−ˉY)2。 (1) 式中:X、Y 为待确定相关程度的2组数据,分别有 m 个元素;i 为从1~m 的数据样本序号;ˉX和ˉY分别为2组数据的平均值; K 为皮尔逊相关系数,其取值为[–1, 1]。
数据间的相关程度由K的绝对值反映,绝对值越大表示数据X与Y间的相关程度越高,由于负荷点电压受母线支撑,其无功来源主要由母线提供,因此,变电站母线与负荷点的电压相关系数,可以通过皮尔逊相关系数来衡量,具体计算公式如下:
CVPVL=cov(VP,VL)σ(VP)σ(VL)。 (2) 式中: VP 和VL分别为变电站母线和负荷点的电压; cov(VP,VL)为VP和VL之间的协方差;σ(VP)和σ(VL)分别为VP和VL数据的标准差。
根据配电网的简化物理模型,开关的状态与相应的节点电压相关系数具有直接的联系。例如,在图1的配网模型中,当开关S2闭合时,变电站母线P2与负荷点N2的电压相关系数要明显高于开关S2断开时的相关系数。换句话说,如果将开关状态和变电站母线与负荷节点的电压相关系数作为随机变量,那么这二者之间必定存在着某种联系,以图1的配网为例,相应的关系如表1所示。
表 1 开关状态与相应电压相关系数的关系等效负荷节点 P1 P2 P3 P4 N1 φ S1 S1, S2, S3 S1, S2, S4 N2 S1, S2 S2 S3 S4 N3 S1, S2, S3 S2, S3 φ S3, S4 在表1中,每一个元素表示变电站母线Pi和负荷点Nj之间的所有开关,φ表示空集,这些开关的状态与电压相关系数CPiNj有着直接的联系。因此,S1、S2、S3、S4开关状态的变化会导致电压相关系数的变化,例如当开关S2状态闭合、开关S3与S4打开时,CVp2VN2的值会明显高于开关S2打开、开关S3与S4闭合时的值。
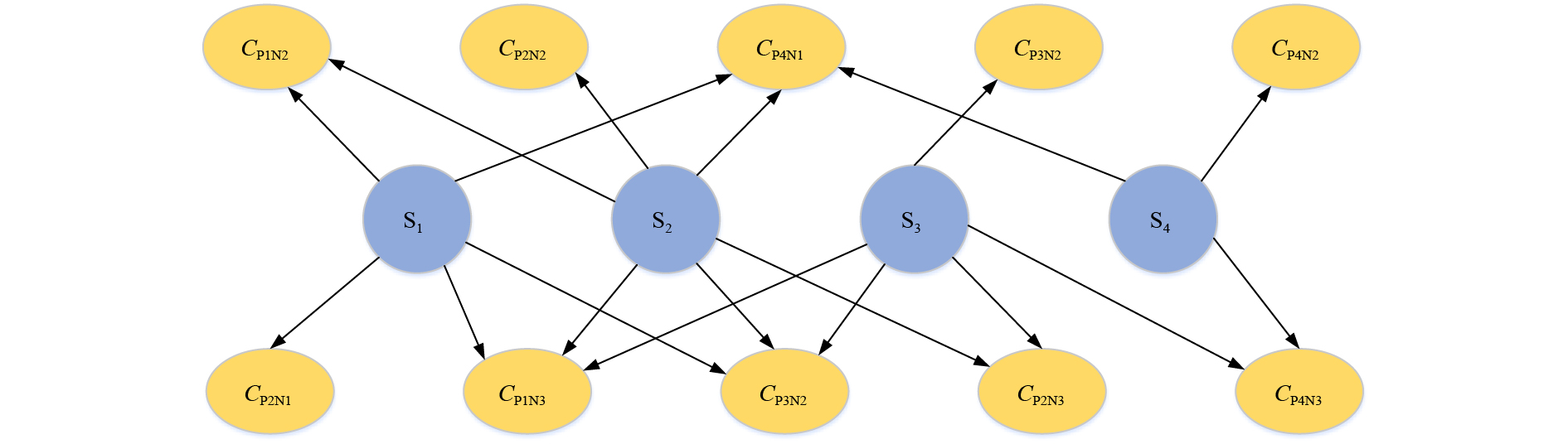
引用贝叶斯网络来表示随机变量之间的因果关系,如图2所示,图中间的圆形顶点表示开关状态的变量而边缘的椭圆形顶点表示电压相关系数的观测变量,其中从圆形顶点到椭圆形顶点的边则表示开关状态与对应的电压相关系数的关系,并且贝叶斯网络定了一个独立的结构:一个节点的概率仅仅依赖于它的父节点,例如,开关S2的状态只会影响CP2N2、CP1N3、CP3N2和CP4N1的值,而不会影响其余节点间的电压相关系数。
1.2 基于信念传播算法的开关运行状态估计
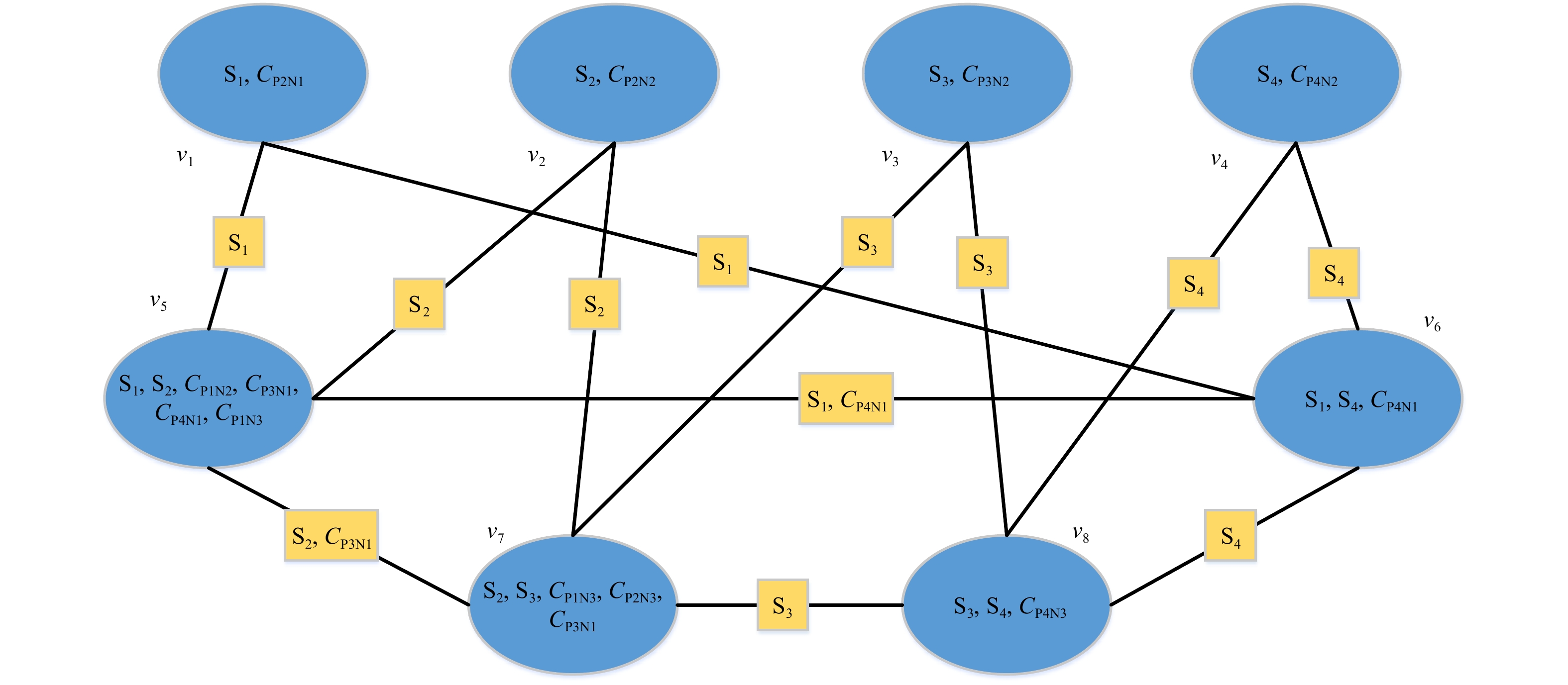
信念传播算法利用节点与节点之间相互传递信息而更新当前整个贝叶斯模型的标记状态,是基于贝叶斯模型的一种近似计算[5]。信念传播算法计算边缘概率分布时首先将贝叶斯模型转为CG模型[6],CG模型是一种间接的概率图模型,每个节点将具有某种联系的随机变量结合到一起,以图2的贝叶斯网络为例,它可以转化为图3的CG模型。
图3所示的CG模型中,每1个蓝色顶点为1组相关变量的集合,顶点之间的边传递着2个顶点之间的交流信息。比如,集群v1的置信度表示随机变量S1以及CP2N1的联合概率分布,而与v1相连的2条边则表示集群v5和v6可以向v1所传递的信息。
对于所转化的CG模型,其节点vi的置信度可表示为bi(vi),而且该置信度与集群vi的局部证据ϕi(vi)以及所有通过相邻边传递给集群vi的信息mji(vi)成正比:
bi(vi)=ziϕi(vi)∏j∈N(i)mji(vi)。 (3) 式中:zi为归一化常数,可使信念的和为1;N(i) 为节点i的一阶邻域,即为与vi相邻的集群。mji(vi)的更新原则如下:
mji←∑vj−ejiϕj(vj)∏k∈Nj∖imkj。 (4) 式中:vj−eji为vj中不包括与vi相同随机变量的其余变量;Nj∖i为除了vi以外与vj相连的所有集群集合。其中,信息在节点之间的传递是双向的,简言之,从集群vi传递到集群vj的信息和vj传递到vi的信息是不同的。根据消息传播和信念更新的不断迭代,直到它们稳定,最后就能从信念中获取相应的概率。
2. 负荷转供数学模型
在对配电网拓扑运行状态进行观测的基础上,变电站全停后的负荷转供优化问题须考虑最大供电恢复能力:在变电站全停的情况下,尽可能多地转移停电负荷。可利用文献[7]的技术设计配电网负荷转供模型。
3. 算例
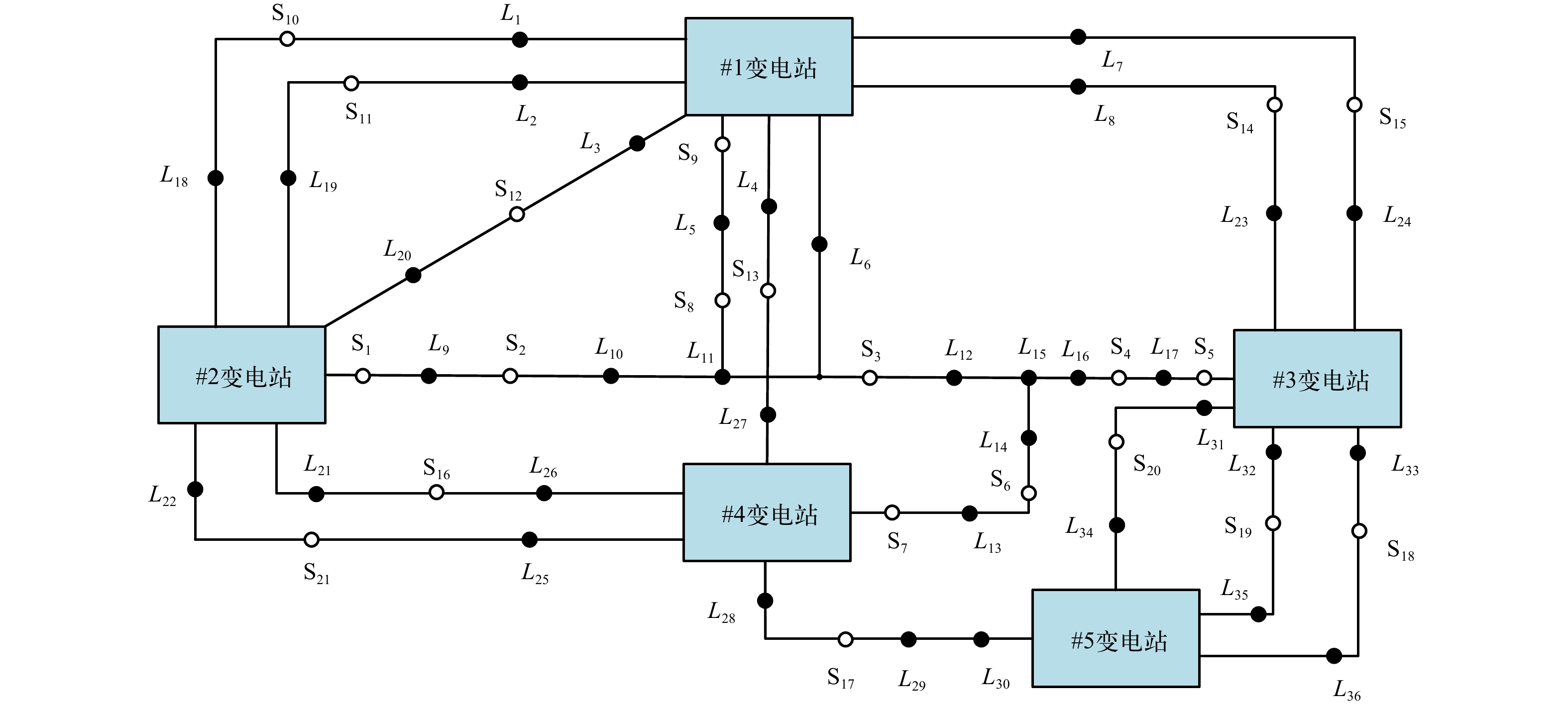
以图4所示的某配网简化接线方式为例,该系统共有5座变电站,21个开关,36个负荷节点,开关状态不一。现在假设由于分布式能源的大量接入引起开关S1~S9的变动而处于不确定状态,研究此情形下1号变电站全停时的负荷转供方案。
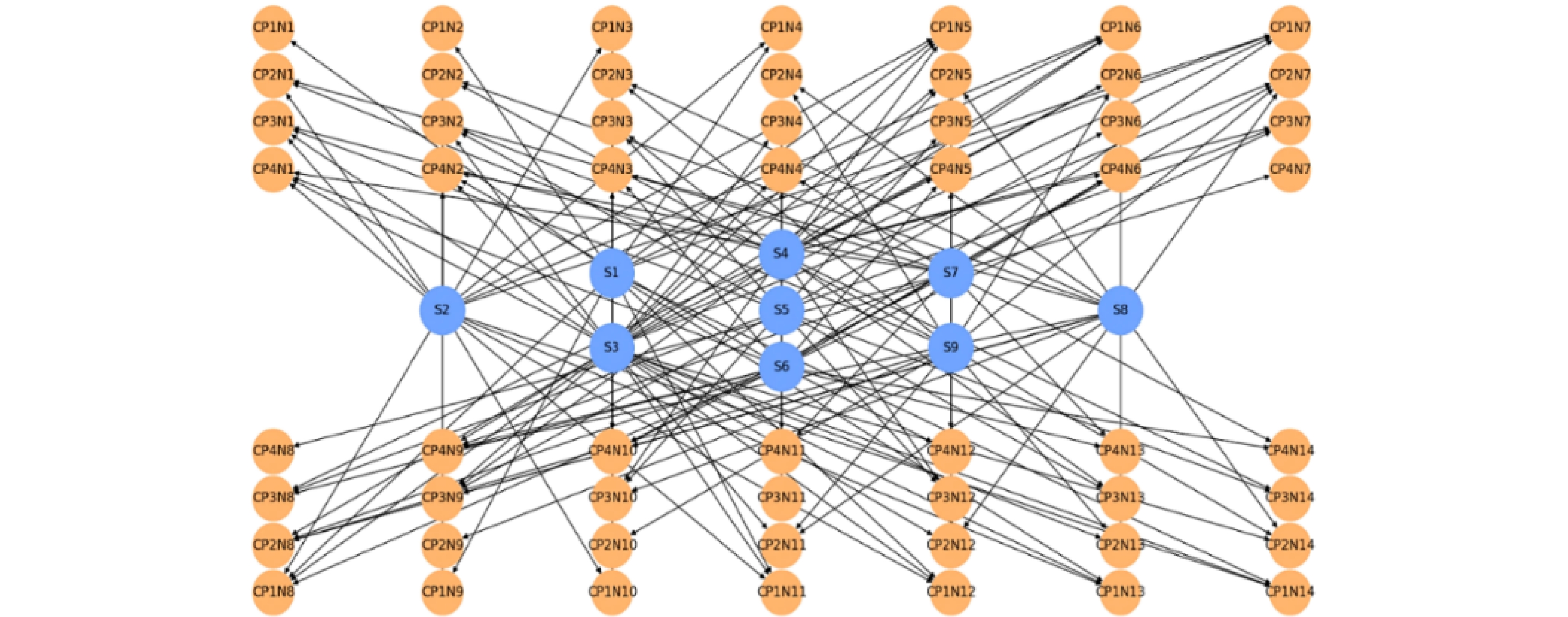
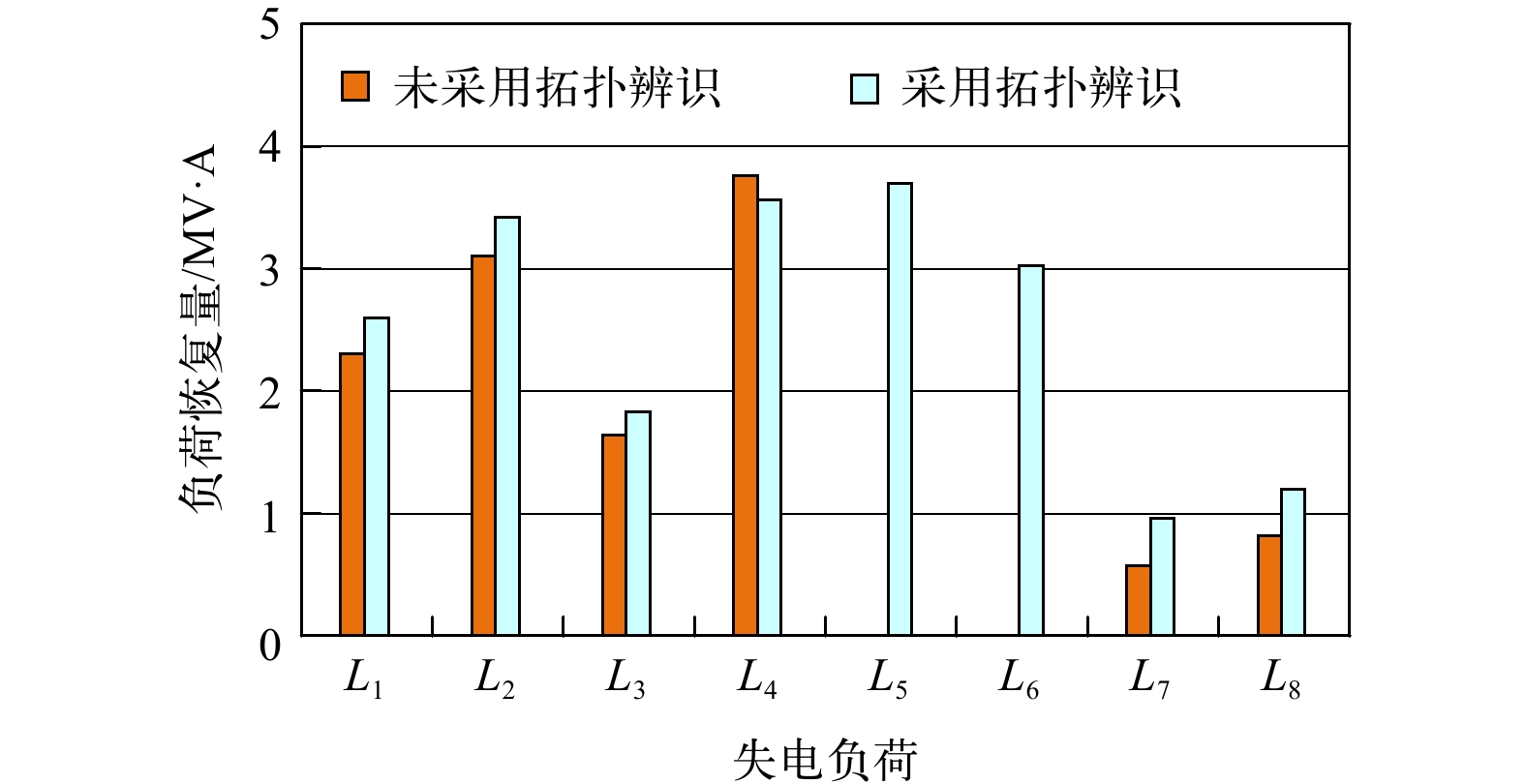
进行1000次配电系统潮流仿真得到原始电压运行数据,假设此时S1~S9的状态估计存在误差。首先根据物理模型图建立S1~S9开关状态与节点电压相关系数的贝叶斯模型,如图5所示,接着运用信念传播算法对贝叶斯模型进行推理,得到开关S6的状态已经发生变动。在此基础上,以遗传算法求解转供模型[8],转供的详细路径如表2所示。可以发现,当未采取准确拓扑运行状态辨识时,开关S6运行状态的变动,直接引起负荷L5与L6转供方案出错,造成无法快速恢复停电负荷供电。采用拓扑辨识后的负荷转供优化对比见图6,因此,本文采取的考虑配网拓扑运行状态的负荷转供技术能够适用于拓扑频繁变动的配网中,提高调度决策的准确性与快速性。
表 2 负荷转供详细路径表负荷 负荷转供路径 未采用拓扑辨识 采用拓扑辨识 L1 L1→S10→L18 L2 L2→S11→L19 L3 L3→S12 L4 L4→S13→L27 L5 转供出错 L5→S8→S3→S6→S7 L6 转供出错 L6→S3→S6→S7 L7 L7→S15→L24 L8 L8→S14→L23 4. 结束语
本文在针对变电站全停时忽视馈线开关状态所造成的转供路径受限问题,提出了利用贝叶斯网络的拓扑运行状态辨识技术。在发生事故后以开关状态和节点电压相关系数的关系将配网的简单物理模型转化为贝叶斯图模型,引入信念传播算法有效迅速地识别配网的拓扑运行方式,并在该识别拓扑的基础上考虑最大可恢复量进行负荷转供,充分计及线路与主变容量的约束以及主变的负载均衡度,有效地解决了传统算法中转供恢复量少、转供决策慢的问题,进一步挖掘配电网的供电潜力,提升配电系统的供电可靠性。
-
表 1 开关状态与相应电压相关系数的关系
等效负荷节点 P1 P2 P3 P4 N1 φ S1 S1, S2, S3 S1, S2, S4 N2 S1, S2 S2 S3 S4 N3 S1, S2, S3 S2, S3 φ S3, S4 表 2 负荷转供详细路径表
负荷 负荷转供路径 未采用拓扑辨识 采用拓扑辨识 L1 L1→S10→L18 L2 L2→S11→L19 L3 L3→S12 L4 L4→S13→L27 L5 转供出错 L5→S8→S3→S6→S7 L6 转供出错 L6→S3→S6→S7 L7 L7→S15→L24 L8 L8→S14→L23 -
[1] 顾明宏,孙为兵,李培培,等. 面对极端扰动事件的城市弹性配电网评估指标体系[J]. 电力系统及其自动化学报,2018,30(7):103−109. [2] 王树元,谢志华,杨柏. 基于新型电力系统地区电网区域备自投研究与应用[J]. 东北电力技术,2023,44(10):49−52. doi: 10.3969/j.issn.1004-7913.2023.10.012 [3] 廖怀庆,刘东,黄玉辉,等. 基于公共信息模型拓扑收缩的配电网转供能力分析[J]. 电网技术,2012,36(6):51−55. [4] Luo Fengzhang, Wang Chenshan, Xiao Jun, et al. Rapid evaluation method for power supply capability of urban distribution system based on N-1 contingency analysis of main-transformers[J]. International Journal of Electrical Power & Energy Systems, 2010,32(10): 1063−1068.
[5] 刘子琳. 信息传播算法在支配集问题中的应用研究[D]. 北方民族大学,2022.DOI: 10.27754/d.cnki.gbfmz.2022.000041. [6] J. Yedidia, W. Freeman and Y. Weiss, "Understanding belief propagation and its generalizations", in Exploring Artificial Intelligence in the New Millennium. 2002(54): 276–286.
[7] 章立宗,吴磊,蒋玮,等. 考虑二次转供的配电网负荷转供方案多目标优选技术[J]. 电网技术,2019,43(7):2321−2328. [8] 江岳文,罗泽宇,程诺. 基于线性化方法的交直流混合配电系统网架规划[J/OL]. 电工技术学报,2023-09-14. DOI: 10.19595/j.cnki.1000-6753.tces.222363.



 下载:
下载: