计量二次回路是关口计量装置的重要组成部分，其误差超差将直接导致计量失准，对发电企业或供电公司造成电量损失。目前计量二次回路仍采用周期校验的方式，中间过程无有效监控措施。且近年光伏电站和风电场数量成倍增加，其地理位置较为偏僻分散，使得现场校验工作更为繁重。加之电力市场化交易对计量准确度的实时要求，保持关口计量二次回路的健康显得尤为重要。因此，须对其进行状态评价和预测以制定合理的检修策略。

文献[1-3]虽然对电能表或计量装置进行了综合状态评价，但大部分仅针对电能表，未对关口计量二次回路开展状态评价或仅采用主观评价法，且未进行健康度趋势预测，无法根据健康度预测结果制定合理检修策略。为此，基于多期历史数据，对计量二次回路进行状态评价，根据评价结果，采用灰色理论对健康度进行合理预测，根据预测结果制定检修策略。为验证健康度趋势预测的合理性，分别采用主客观综合评价法和层次分析法进行状态评价，基于状态评价结果，进行灰色预测。

1.   状态评价模型及量化方法

对影响关口计量二次回路的各因素分类分析，包括现场压降误差、运行时间、回路长度、配置情况、在线压降误差。

1.1   现场压降误差

现场实测压降误差是计量二次回路状态最直接的反映。最近2次现场检验数据参考意义较大，将实测压降误差量化处理。

式中： $\left|{l}_{1}\right|$为误差上限； ${x}_{11}$、 ${x}_{12}$为近2次现场检测误差数据； ${S}_{1}\geqslant 0$。

1.2   运行时间

计量二次回路的状态与其运行时间密切关联。运行时间过长容易出现线路老化，接口松动，中间转接处或接口处氧化，导致接触电阻增加，从而导致回路压降异常。

式中： ${t_2}$为运行时间； ${S}_{2}\geqslant 0$。

1.3   导线长度量化

回路长度对压降误差有直接和间接影响，同等条件下，回路越长，回路上的压降越大。

式中： ${l_3}$为导线长度； ${S}_{3}\geqslant 0$。

1.4   二次回路基本配置量化

选定影响最大的3个因素，导线截面积 ${x}_{4}$、中间接头数 ${y}_{4}$和开关类型 ${\text{z}}_{4}$。

式中： $a$、 $b$、 $c$为0.8、0.95和0.85。

1.5   二次回路在线压降误差量化

二次回路在线压降误差可依据国网河南电力公司安装的远程校验装置误差数据获取，设其为 ${x}_{5}$。

式中： ${l}_{5}$为误差限值。

1.6   状态量归一化处理

对各分项状态量归一化及量化处理，将最终评价值统一转换到0～100的标准值。

1.7   状态评价模型

根据1.1～1.6的分析，构建二次回路总体状态评价模型：

式中： ${W}_{i}$为分项权重， $\displaystyle\sum_{i=1}^{5}{W}_{i}=1$。

2.   状态评价方法

2.1   主客观评价法

主客观评价法综合序关系方法和熵权法^[4]，权重值既包含行业内权威专家的意见，也综合了客观历史数据中隐藏的规律，评价结果可信度更高。

2.1.1   序关系法

序关系方法中，采用权威专家对各指标权重进行重要程度对比，通过两两对比，得到序关系序列表，进而求得专家评定的权重值，主要流程如下。

（1）各指标两两对比

权威专家对各指标两两对比分析，根据重要程度可得序关系序列：

令 ${{\alpha }_{k-1}^{*}}/{{\alpha }_{k}^{*}}={r}_{k}$， $\left(k=n,n-1,n-2,\cdots, \mathrm{3,2}\right)$。

${r_k}$值根据重要程度对比，可取值为1.0，1.2，1.4，1.6，1.8。其中：数值1.8表示权重 ${\alpha ^{\text{*}}_{k - 1}}$比 ${\alpha ^{\text{*}}_k}$极端重要。

（2） ${{{\alpha }^{}}_{k}^{*}}$的计算

上步中 ${{\alpha }_{k-1}^{*}}\succ {{\alpha }_{k}^{*}}$表示 ${{\alpha }_{k-1}^{*}}$的重要性不小于 ${{\alpha }_{k}^{*}}$。令 ${r}_{1}=1$，进一步计算可得权重值：

2.1.2   熵权法

通过对历史数据分析，从历史数据中提取特征量，特征量中包含数据本身的内在规律，客观性强。其主要流程如下。

（1）原始数据处理

根据参与计算的原始历史数值可建立矩阵 ${{X}}=\{x_{ij}\}$，将其标准化处理后得到 ${{Y}}=\{y_{ij}\}$，具体计算如下：

式中： ${x}_{ij}$、 ${y}_{ij}$分别为矩阵X和Y的第i行第j列元素； ${X}_{j}$为矩阵第j列的各元素。

（2）根据公式求取信息熵

式中： ${E}_{j}$为信息熵； $p_{ij}$为指标比重，且有 ${p}_{ij}= {y}_{ij}/\displaystyle\sum_{i=1}^{n}{y}_{ij}$。

（3）求取权重

式中：n为指标个数。

2.1.3   主客观分析结合

权威专家主观评价的序关系法与以数据自身特点和内在逻辑关系为基础的熵权法相结合，形成互补，得到最终权重值。

最终权重值 ${W}_{i}$计算如下：

式中： ${\alpha }_{j}^{*}$、 ${\varepsilon }_{i}$分别为序关系和熵权法求解的权重值。

2.2   层次分析法

层次分析法可将无法定量分析的各权重指标，通过对各影响因素的重要性比对，建立定量关系，使各因素对目标的影响明确化、清晰化。其主要流程如下。

2.2.1   构造判定矩阵并进行一致性判定

根据各因素间的重要程度关系，构造目标矩阵A。并对A进行一致性判定。判定公式如下：

式中： ${\lambda }_{\max}$为判定矩阵的最大特征值； ${R}_{I}$与判定矩阵大小 $n$有关，其值可以通过查询获得，如表1所示。若 ${C}_{R} < 0.1$可认为判定是合理的。

表  1  层次分析法一致性要求

$n$	1	2	3	4	5	6	7	8
${R}_{I}$	0.00	0.00	0.58	0.90	1.12	1.24	1.32	1.41

下载: 导出CSV 

| 显示表格

2.2.2   求取权重值

矩阵A不一定是一致矩阵，当满足 ${C}_{R} < 0.1$时，说明其一致性在合理范围内。此时无法直接求取最大特征值，可采用等效方法求取，具体如下：

设矩阵 $A(m \times n)=\{a_{ij}\}$，则有 $\overline{{w}_l}=\sqrt[\leftroot{-1}\uproot{12}{n}]{\displaystyle\prod_{j=1}^{n}{a}_{ij}}$。对 $W$进行标准化后，即可求得权重向量。

3.   基于灰色理论的计量二次回路健康度预测

计量二次回路的状态评价结果可用来制定其检修策略，将周期校验模式有依据地、科学地向问题导向校验模式转变，提出一种基于灰色GM(1,1)模型的二次回路健康度趋势预测方法^[5]。

以近期按月获取的数据为例，假定通过近期动态数据进行状态评价得到 $N$个状态评价值，基于此即可进行GM(1, 1)灰色预测。将此 $N$个值用 ${h}^{(0)}(n),n=1,\cdots ,N$表示。并将相邻数值累加后得到新的数值记为：

可构造GM(1, 1)方程如下：

式中： ${\text{z}}^{\left(1\right)}(n)$为在 ${h}^{\left(1\right)}(n)$基础上利用相邻数据生成的数值。其计算公式如下：

根据采用历史数据求得的 $N$个健康度值，可求取GM(1, 1)中的发展系数 $a$和灰色作用量 $b$，一般采用最小二乘法进行计算。假设：

式中： ${1}_{N}$为 $N$个数值为1的向量。由此可以计算出GM(1, 1)中的 $a$、 $b$ 2个参数，计算方法如下：

将GM(1, 1)转化为微分形式，可得：

求解可得：

根据求得的解，进一步计算累加数列为：

式中： $n\geqslant 0$； ${h}^{\left(0\right)}(1)$为采用主客观赋值法或层次分析法得到的状态评价值。由前面采用最小二乘法计算得到的 $a$、 $b$代入上式后可得累加数列的预测值。进而可计算出根据历史数据代入得到的预测值。计算公式如下：

可设定预测数，根据多组预测值，判断计量二次回路的健康度走势，进而制定对应检修策略。

将 ${h}^{\left(0\right)}(x+1)$加入预测参数组，去掉 ${h}^{\left(0\right)}(1)$。由此可建立新的新陈代谢GM(1, 1)模型。改进模型如下所示：

4.   河南电网工程应用实例

为验证改进灰色理论预测的准确性，选取河南某市35条关口计量二次回路为研究对象。收集每条回路的基本参数、配置、历史现场检测情况，并提取全时在线监测系统中二次回路相关状态参数。选取2022年6月到2023年6月各关口计量二次回路的数据。首先从现场压降误差、运行时间、回路长度、配置情况、在线压降误差等几个方面对数据进行标准化、归一化处理，代入公式（1）～（5）求得指标项具体值，然后采用2种方法分别进行状态评价及灰色预测，后续现场校验中发现该市35条线路中，实际有3条线路误差偏高。

4.1   主客观评价法及预测结果

首先采用序关系分析法，采用公式（6）～（8）对已归一化处理的标准数据进行评价。建立信息熵矩阵，并将数据代入公式（9）～（12）得到主客观评价结果的权重值。将35组数据，每组通过2022年6月至2023年6月得到的状态评价值分别作为灰色预测的输入参数，代入公式（15）～（23）进行预测，得到预测结果如表2所示。

表  2  基于主客观评价预测结果

回路数	预测值较低回路数	实际误差偏高数
35	4	3

下载: 导出CSV 

| 显示表格

4.2   层次分析法及预测结果

同样地，利用已有历史数据和监测值，通过层次分析法进行状态评价，代入公式（13）～（14）得到历史状态价值后，将其作为输入变量得到最新预测值。其结果如表3所示。

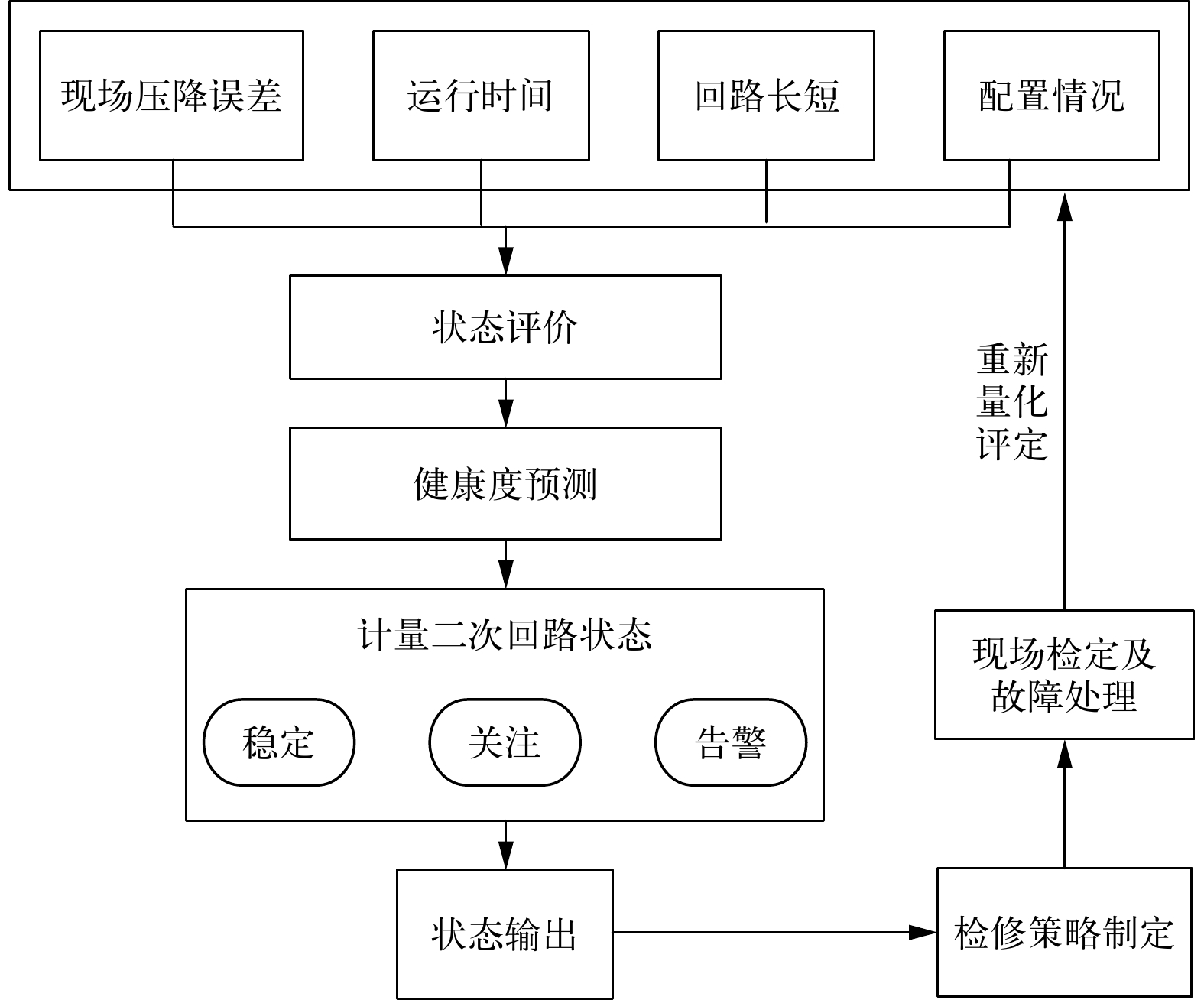
表  3  基于层次分析法预测结果

回路数	预测值较低数	误差偏高数
35	4	3

下载: 导出CSV 

| 显示表格

根据预测结果，进行检修策略调整，如图1所示。

图  1  健康度评价及检修策略流程图

下载: 全尺寸图片 幻灯片

4.3   综合分析

基于主客观综合法和层次分析法评价结果进行的健康度预测结果基本一致。因为本身综合评价结果的变化趋势是一致的，只是2种评价结果的侧重点虽各有不同，但基础数据是一致的，数据的变化趋势一致，因此预测结果相似。

从表2和表3中可知，2种状态评价结果的健康度评价的预警值设定不一致。这说明，一方面2种方法在数值上是存在差异的，但通过调整警戒值，其结果相符。其次，预警值的设置可以动态微调，以满足对异常回路的筛选要求。

警戒异常的回路数与实际误差偏高数不完全一致。为了防止漏判异常回路，需将预警值适当设置偏高。误差偏高数不是一开始就知道的，需要根据预测结果，进一步筛选，进而制定现场检测计划，根据现场检验计划确定该回路是否压降偏高或超差。

2种状态评价得到的灰色预测结果一致，且与计量回路的实际情况基本相符。验证了本文提出的将改进灰色理论应用到计量二次回路健康度预测的合理性。

5.   结束语

“双碳”背景下，关口计量点数量成倍增长，二次计量回路也随之增加，为应对现场工作量数倍增长及电力市场化交易对计量装置误差高稳定性的新要求，本文提出采用主客观评价法和层次分析法进行状态评价，并根据评价结果进行改进新陈代新GM(1, 1)预测的方法。根据预测结果值，可灵活调整二次计量回路现场检验策略。采用河南某市35条关口计量二次回路数据进行预测分析，预测结果与实际相符，证明改进GM(1, 1)方法可根据历史参数获得的状态评价值，准确预测其变化趋势。同时，预警值的设置需要积累一定的经验，后期将开展全省范围内计量二次回路状态评价及健康度趋势预测，通过不断地积累经验，模型将更准确合理。