基于模型预测控制算法的NPC三电平逆变器

钱金跃; 杨玉锐; 姚强; 崔寅; 陶琨; 吴伟健; 陆佳晨; 缪薇; 李德猛

doi:10.13882/j.cnki.ncdqh.2022.08.007

基于模型预测控制算法的NPC三电平逆变器

国网浙江省电力有限公司平湖市供电公司, 浙江平湖 314200

详细信息

作者简介:
钱金跃(1994—), 男, 助理工程师, 逆变器控制研究

中图分类号: TM475
计量
- 文章访问数: 0
- HTML全文浏览量: 0
- PDF下载量: 0
出版历程
- 收稿日期: 2022-05-24
- 刊出日期: 2022-08-09

NPC Three-Level Inverter Based on Model Predictive Control Algorithm

Pinghu Power Supply Company, State Grid Zhejiang Electric Power Co., Ltd., Zhejiang Pinghu 314200, China

摘要

摘要:
应用于二极管箝位型（neutral point clamped，NPC）三电平逆变器的空间矢量脉宽调制（space Vector pulse width modulation，SVPWM）方法，由于零矢量参与调制或滚动优化，无法有效降低共模电压（commonmode voltage，CMV），且运算时间长。针对上述问题，提出一种综合考虑中点电位、开关频率和共模电压的模型预测控制算法。首先，建立NPC三电平逆变器的负载电流、中点电位离散化数学预测模型。然后，构建中点电位、开关频率、CMV的多约束目标函数，滚动筛选最优矢量作用NPC三电平逆变器，降低共模电压且减少运行时间。最后，在MATLAB/SIMULINK平台搭建仿真模型，并对算法的运行性能进行验证。
- NPC三电平逆变器 /
- 中点电位 /
- 共模电压 /
- 模型预测控制 /
- 仿真
Abstract:
The space vector pulse width modulation (SVPWM) method applied to the neutral point clamped (NPC) three-level inverter cannot effectively reduce the common mode voltage (CMV) due to the zero vector participating in the modulation or rolling optimization, and the operation time is long. To solve the above problems, a model predictive control algorithm considering neutral point potential, switching frequency and common mode voltage is proposed in this paper. Firstly, the discrete mathematical prediction model of load current and neutral point potential of NPC three-level inverter is established. Then, the multi constraint objective functions of neutral point potential, switching frequency and CMV are constructed, and the optimal vector is selected to act on NPC three-level inverter, reducing common mode voltage and running time. Finally, the simulation model is built on matlab/simulink platform, and the performance of the algorithm is verified.
- NPC three-level inverter /
- neutral point potential /
- common mode voltage /
- model predictive control /
- simulation

HTML全文

二极管箝位型(Neutral point clamped, NPC)三电平逆变器以其低谐波输出、低开关损耗、低器件耐压水平等优点, 被广泛应用于大功率并网控制系统、电力传动系统^[1]。但是NPC型三电平逆变器存在固有缺点, 当中点电位平衡, 同一桥臂上下两个开关管仅承受一半的直流电压; 当中点电位不平衡, 同一桥臂上下两个开关管分别承受不同电压, 将降低开关管使用寿命, 甚至烧毁开关管, 并增加交流侧输出电压的谐波含量。因此, 如何有效控制中点电位平衡一直是学术界研究热点。

软件控制和硬件改造是控制NPC型三电平逆变器中点电位平衡的两种方法。文献[2]研究了合理分配冗余小矢量控制中点电流流向以实现中点电位平衡, 但计算相对复杂, 执行时间较长。文献[3]通过额外增加桥臂的硬件方法控制中点电位, 但是成本昂贵、占地面积大。文献[4]采用的算法虽然减少计算量, 但是器件具有较高的开关频率, 忽视了开关损耗。

应用于驱动领域的NPC三电平逆变器较为突出问题为高频共模电压(common-modevoltage, CMV), 其在电动机转轴上感应高振幅轴电压并产生轴电流, 破坏绝缘、腐蚀电机、缩短寿命^[5]。此外, 高频漏电流(高频CMV产生)会产生电磁干扰, 影响设备正常运行^[6]。

综合考虑成本和体积因素, 软件控制是首选。近年来, 模型预测控制(model predictive control, MPC)被广泛应用于现代电力电子领域^[7], 其响应速度快, 适用于多变量和非线性系统, 在许多领域都被证明其优于传统方法。其在NPC型三电平逆变器中点电位的不平衡控制中, 主要以离散化系统数学模型为基础, 根据历史输出预测未来输出, 并结合目标函数滚动筛选最优开关状态的控制算法。

本文提出一种综合考虑中点电位、开关频率和共模电压的模型预测控制算法。首先, 建立NPC三电平逆变器的负载电流、中点电位离散化数学预测模型。然后, 基于MPC适用于多变量和非线性系统, 构建中点电位、开关频率、CMV的多约束目标函数, 滚动筛选最优矢量作用NPC三电平逆变器, 降低共模电压且减少运行时间。最后, 在MATLAB/SIMULINK平台搭建NPC三电平逆变器仿真模型, 并对算法的运行性能进行验证。

1. NPC三电平逆变器

1.1 工作原理

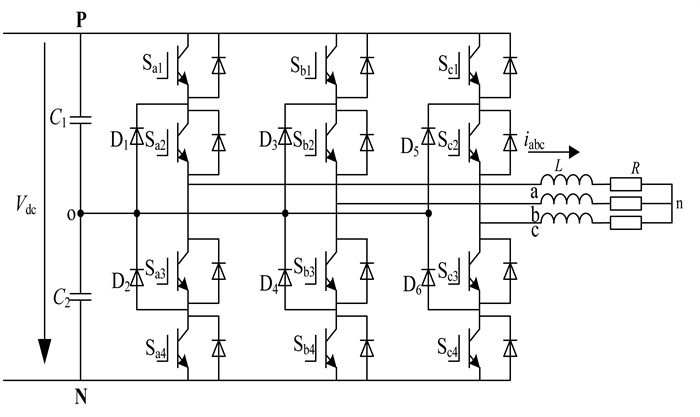
RL负载的NPC三电平逆变器拓扑结构如图 1所示, 其中每个桥臂包含四个IGBT开关器件和两个箝位二极管。直流侧两个电容中点(记作“O”点)连接两个箝位二极管的中点, 其中“O”点为零电位参考点。

图 1 NPC三电平逆变器拓扑结构

下载: 全尺寸图片幻灯片

由图 1可知, 每相桥臂的开关S_a1和S_a3(S_a2和S_a4)不能同时导通, 因此每相桥臂只有三种开关状态, 即P、O、N状态。假设用{1, 0, -1}表示上述状态, 输出电压用v_ao表示, “1”代表v_ao为V_dc/2, “0”代表v_ao为0, “-1”代表v_ao为-V_dc/2。定义开关函数如式(1)所示:

$S_i=\left\{\begin{array}{l} 1, \mathrm{~S}_{i 1}, ~ \mathrm{~S}_{i 2} \text { 通, } \mathrm{S}_{i 3}、 \mathrm{~S}_{i 4} \text { 断 } \\ 0, \mathrm{~S}_{i 2}, ~ \mathrm{~S}_{i 3} \text { 通, } \mathrm{S}_{i 1}、 \mathrm{~S}_{i 4} \text { 断。 } \\ -1, \mathrm{~S}_{i 1}, ~ \mathrm{~S}_{i 2} \text { 通, } \mathrm{S}_{i 3}、 \mathrm{~S}_{i 4} \text { 断 } \end{array}\right.$

(1)

式中: i =a, b, c。

为了简述表达每相的三个工作状态与v_ao的关系, 上述分析如表 1所示。

表 1 每相工作状态与输出电压v_ao

工作状态	开关状态				输出电平
工作状态	S_α1	S_α2	S_α3	S_α4	输出电平
P	1	1	0	0	V_dc/2
O	0	1	1	0	0
N	0	0	1	1	-V_dc/2
注：α =a, b, c

下载: 导出CSV

| 显示表格

1.2 数学模型

由图 1可知, 直流侧两个电容中点“O”为零电位参考点, 因此αβ坐标系下的三相输出电压为:

$u_{\alpha, \mathsf{β}}=\frac{2}{3}\left(u_{\mathrm{an}}+\alpha u_{\mathrm{bn}}+\alpha^2 u_{\mathrm{cn}}\right) \text { 。 }$

(2)

式中: α =e^j2π/3; u_α_, _β= u_α + ju_β, u_α和u_β是αβ坐标系下u_α_, _β的实部与虚部; u_an、u_bn、u_cn是abc坐标系下三相输出电压, 且∈{V_d _c/2, 0, -V_d _c/2}。

同理, αβ坐标系下的三相负载电流为:

$i_{\alpha, \mathsf{β}}=\frac{2}{3}\left(i_\alpha+\alpha i_{\mathrm{b}}+\alpha^2 i_{\mathrm{c}}\right) \text { 。 }$

(3)

式中: α = e^j2π/3; i_{α, β}= i_α + ji_β, i_α和i_β是αβ坐标系下i_α_{, β}的实部与虚部; i_α、i_b、i_c是abc坐标系下三相负载电流。

因此, 连续时域下的NPC型三电平逆变器数学模型为:

$u_{\alpha, \beta}=L \frac{\mathrm{~d} i_{\alpha, \mathsf{β}}}{\mathrm{d} t}+R i_{\alpha, \mathsf{β} \circ}$

(4)

式中: R为负载电阻; L为负载电感。

在一个采样周期T_s内, 采用一阶欧拉公式(式(6)离散化式(5), 可得第(k + 1)时刻的预测电流, 如式(7)所示。

$\frac{\mathrm{d} x(t)}{\mathrm{d} t}=\frac{x(k+1)-x(k)}{T_{\mathrm{s}}}。$

(5)

$\begin{gathered} i_{\alpha, \beta}^p(k+1)=i_{\alpha, \mathsf{β}}(k+1)= \\ {\left[1-\frac{T_{\mathrm{s}} R}{L}\right] i_{\alpha, \beta}^p(k) \frac{T_{\mathrm{s}}}{L} u_{\alpha, \mathsf{β}}(k)}。 \end{gathered}$

(6)

式中: 上标“p”为预测值; k为第k个采样周期; i_α_{, β}(k)为第k次采样电流。

2. 中点电位不平衡及开关频率

2.1 不平衡分析

不对称的三相负载、不同的电容参数、不同空间电压矢量作用下不对称的流出和流入电流都会导致直流侧上下两个分压电容的不平衡。相关文献详细分析了零矢量、小矢量、中矢量和大矢量对中点电位不平衡的影响, 并得出结论: 中点电位波动的本质是由于小矢量或中矢量作用下产生中点电流i_o, 且i_o与i_a、i_b、i_c的关系为:

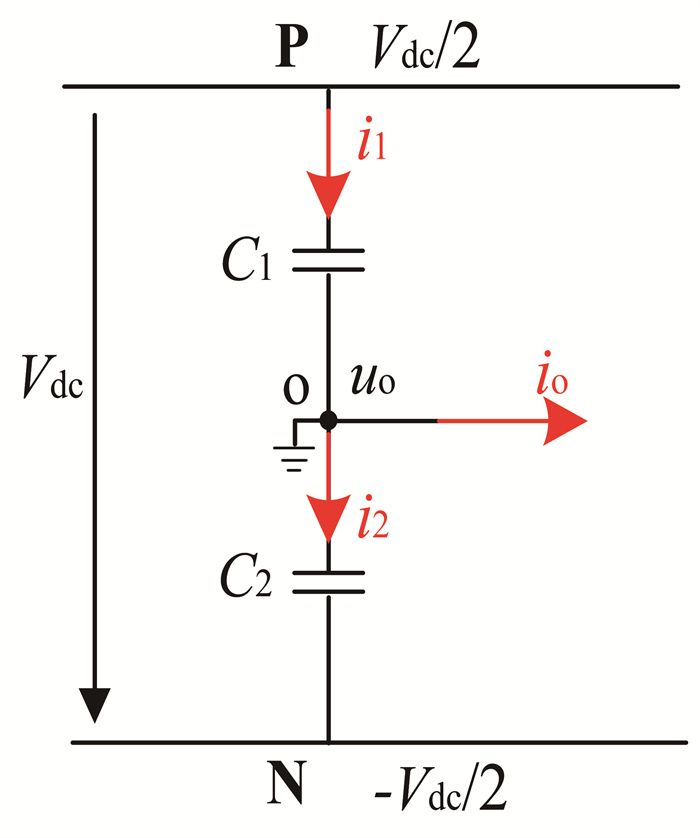
$i_o=\left(1-\left|S_{\mathrm{a}}\right|\right) i_a+\left(1-\left|S_{\mathrm{b}}\right|\right) i_{\mathrm{b}}+\left(1-\left|S_{\mathrm{c}}\right|\right) i_{\mathrm{c}}。$

(7)

由1.1节可知, 中点“O”为零电位参考点, 故u_o为零电位点。直流侧上下两个分压电容流过的电流方向及中点电流的流向如图 4所示, i₁表示流过上分压电容电流, i₂表示流过下分压电容电流, i_o表示中点电流, 以图中所标方向为正方向。

假设C₁ = C₂ = C, 则C₁承受的电压为v_dc1, C₂承受的电压为v_dc2, 则i₁和i₂可表示为:

$i_1=C_1 \frac{\mathrm{~d}\left(V_{\mathrm{dc}} / 2-u_o\right)}{\mathrm{d} t} 。$

(8)

$i_2=C_2 \frac{\mathrm{~d}\left(u_o-V_{\mathrm{dc}} / 2\right)}{\mathrm{d} t}。$

(9)

在零电位参考点“O”处应用基尔霍夫电流定律, 故i_o可表示为:

$i_1-i_2=C \frac{\mathrm{~d}\left(V_{\mathrm{dc}} / 2-u_o\right)}{d t}-C \frac{\mathrm{~d}\left(u_o-V_{\mathrm{dc}} / 2\right)}{d t} i_{o \circ}$

(10)

将式(7)代入式(10), 并应用式(6)离散化, 可得:

$\begin{gathered} u_o^p(k+1)=u_o(k)- \\ \frac{T_{\mathrm{s}}}{2 C} \cdot\left[\left(1-\left|S_{\mathrm{a}}\right|\right) i_a+\left(1-\left|S_{\mathrm{b}}\right|\right) i_{\mathrm{b}}+\left(1-\left|S_{\mathrm{c}}\right|\right) i_{\mathrm{c}}\right]。 \end{gathered}$

(14)

其中: u_o(k)是第k时刻零电位值。

因此, 根据式(11)可预测第(k + 1)时刻的零电位值。

2.2 开关频率分析

降低开关频率通过选择第k - 1时刻和第k时刻开关状态变换最少的空间电压矢量, 减少器件频繁投切的次数, 延长器件使用寿命。定义从第k - 1时刻到第k时刻的一个周期内开关切换次数为开关频率, 可表示为:

$\begin{gathered} \mathrm{S}_{\text {swictech }}=\left|S_{\mathrm{a}}(k)-S_{\mathrm{a}}(k-1)\right|+\left|S_{\mathrm{b}}(k)-S_{\mathrm{b}}(k-1)\right|+ \\ \left|S_{\mathrm{c}}(k)-S_{\mathrm{c}}(k-1)\right|。 \end{gathered}$

(12)

其中: S_j(k)(j = a, b, c)表示第k时刻的开关状态, S_j(k -1)表示第(k -1)时刻的开关状态。

2.3 共模电压分析

由表 1可知, 输出相电压可由开关函数表示为

$\left\{\begin{array}{l} u_{\mathrm{ao}}=\frac{1}{2} V_{\mathrm{dc}} S_{\mathrm{a}}, \\ u_{\mathrm{bo}}=\frac{1}{2} V_{\mathrm{dc}} S_{\mathrm{b}}, \\ u_{\mathrm{co}}=\frac{1}{2} V_{\mathrm{dc}} S_{\mathrm{c}}。 \end{array}\right.$

(13)

在图 1中, 定义“n”和“o”之间的电位差为共模电压(u_c_om), 理想情况下, 三相负载电流i_a +i_b +i_c=0, 根据基尔霍夫电压定律可将u_c_om可表示为

$u_{c\mathrm{om}}=\frac{1}{3} V_{\mathrm{dc}}\left(u_{\mathrm{ao}}+u_{\mathrm{bo}}+u_{\mathrm{co}}\right) \text { 。 }$

(14)

将式(13)代入式(14), u_com可表示为

$u_{c\mathrm{om}}=\frac{1}{6} V_{\mathrm{dc}}\left(S_{\mathrm{a}}+S_{\mathrm{b}}+S_{\mathrm{c}}\right) 。$

(15)

由式(15)可知, u_com由开关状态决定, 每个开关状态对应的u_com如表 2所示。

表 2 开关状态和共模电压之间的关系

矢量	开关状态	u_com
大矢量	[1 -1 -1] [-1 1 -1] [-1 -1 1]	-V_dc/6
大矢量	[1 1 -1] [-1 1 1] [1 -1 1]	V_dc/6
中矢量	[1 0 -1] [0 1 -1] [-1 1 0]	0
中矢量	[-1 0 1] [0 -1 1] [1 -1 0]	0
正小矢量	[0 -1 -1] [-1 0 -1] [-1 -1 0]	-V_dc/3
正小矢量	[1 1 0] [0 1 1] [1 0 1]	V_dc/3
负小矢量	[1 0 0] [0 1 0] [0 0 1]	V_dc/6
负小矢量	[0 0 -1] [-1 0 0] [0 -1 0]	-V_dc/6
零矢量	[-1 -1 -1][1 1 1]	-V_dc/2 V_dc/2
零矢量	[0 0 0]	0

下载: 导出CSV

| 显示表格

由表 2可知, 27个开关状态共对应7个不同的u_com, 最小值为0, 最大值为|V_dc/2|。

3. 模型预测控制

3.1 目标函数

MPC算法的灵活性和适用性主要表现为可将多个控制目标、控制变量及约束条件整合在一个目标函数, 但是不同的控制目标存在不同的数量级或者优先级, 因此需要在目标函数中引入权重因子λ, 本文定义中点电位, 开关频率以及共模电压的权重因子分别为λ₁、λ₂和λ₃。对于NPC型三电平逆变器, 保证中点电平是其正常运行的关键, 故λ₁ ≠0, 考虑控制优先级顺序(依次为中点电位控制、CMV限制、开关频率), 故设置λ₁ > λ₂ = λ₃ > 0。

综合上述分析, 本文定义目标函数为:

$\begin{gathered} g=\left|i_a^*(k+1)-i_a^{\mathrm{p}}(k+1)\right|+\left|i_\mathsf{β}^*(k+1)-i_\mathsf{β}^{\mathrm{p}}(k+1)\right|+ \\ \lambda_1\left|u_{\mathrm{o}}^{\mathrm{p}}(k+1)\right|+\lambda_2 S_{\text {swicteh }}+\lambda_3\left|u_{c\text {om }}\right|_{\circ} \end{gathered}$

(16)

式中: $i_a^{\mathrm{p}}(\mathrm{k}+1)$ 、 $i_\mathsf{β}^{\mathrm{p}}(k+1)、 ~ i_\mathsf{β}^*(k+1)$ 和 $i_\mathsf{β}^*(k+1)$ 分别是αβ坐标系下k + 1时刻的负载电流预测值和参考值; λ₁、λ₂和λ₃分别是3个不同约束的权重因子; S_swictch如式(15)所示; u_c_om如式(20)所示。

3.2 控制策略

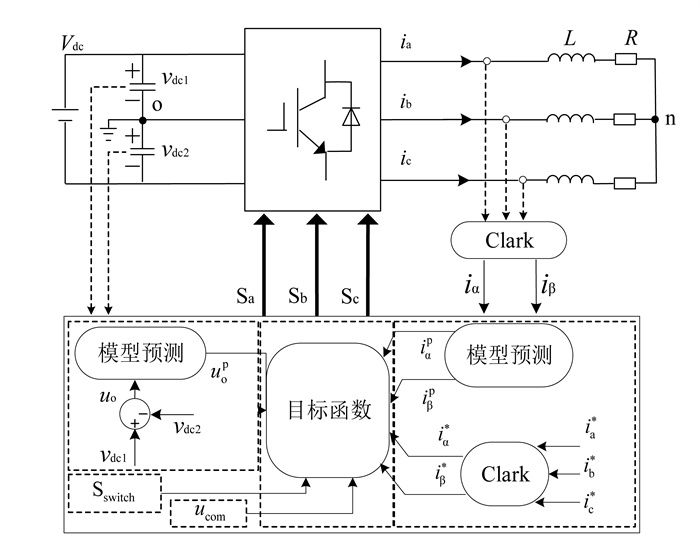
图 3为NPC型三电平逆变器模型预测控制算法结构框图。

图 2 不平衡分析

下载: 全尺寸图片幻灯片

图 3 MPC算法结构框图

下载: 全尺寸图片幻灯片

4. 仿真验证

在分析上述工作原理、数学模型、中点电位不平衡、开关频率和共模电压的基础上, 结合模型预测控制策略, 在MATLAB/SIMULINK平台搭建基于模型预测控制算法的NPC三电平逆变器仿真模型, 并对算法的运行性能进行验证。仿真参数如表 3所示。

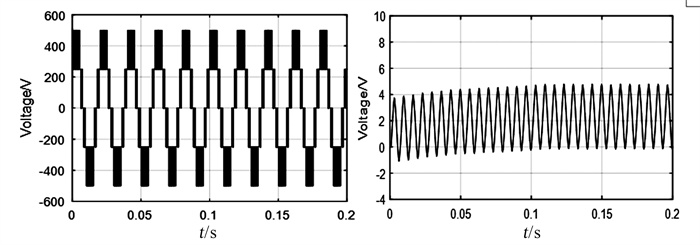
表 3 主要参数

参数	数值	参数	数值
直流侧电压/V	500	参考电流频率/Hz	50
电容/μ F	3300	采样频率/kHz	10
负载电感/mH	5	λ₁	1.5
负载电阻/Ω	20	λ₂	0.5
参考电流/A	12	λ₃	0.5

下载: 导出CSV

| 显示表格

基于模型预测控制算法的稳态线电压和中点电位如图 4所示, 从图中可以看出中点电位稳定在0~5 V。

图 4 稳态线电压和中点电位波形图

下载: 全尺寸图片幻灯片

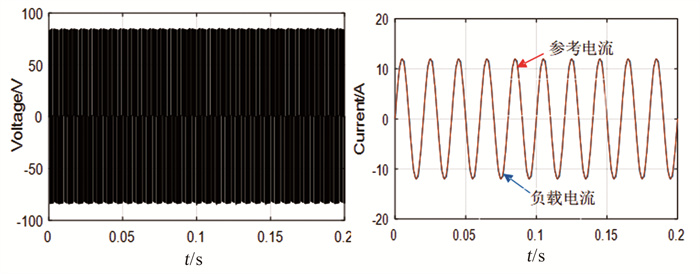
基于模型预测控制算法的共模电压如图 5所示, 从图中可以看出该算法限制共模电压幅值范围为|V_dc/6|, 且负载电流能快速跟踪参考电流。

图 5 共模电压、负载电流与参考电流的对比图

下载: 全尺寸图片幻灯片

表 4对比SVPWM与MPC的运行时间。相比SVPWM, MPC单个周期的运行时间明显下降, 大概节约33%。相同硬件条件下, 相比SVPWM, MPC运行效率更高。

表 4 运行时间对比

	运行时间/μ s	降低率（对比SVPWM）/%
SVPWM	19.78	-
MPC	13.26	33

下载: 导出CSV

| 显示表格

5. 结束语

本文提出一种综合考虑中点电位、开关频率和共模电压的模型预测控制算法。在NPC三电平逆变器的负载电流、中点电位离散化数学预测模型的基础上构建中点电位、开关频率、CMV的多约束目标函数, 滚动筛选最优矢量作用NPC三电平逆变器, 实现降低共模电压, 并减少运行时间。

图 1 NPC三电平逆变器拓扑结构

下载: 全尺寸图片幻灯片

图 2 不平衡分析

下载: 全尺寸图片幻灯片

图 3 MPC算法结构框图

下载: 全尺寸图片幻灯片

图 4 稳态线电压和中点电位波形图

下载: 全尺寸图片幻灯片

图 5 共模电压、负载电流与参考电流的对比图

下载: 全尺寸图片幻灯片

表 1 每相工作状态与输出电压v_ao

工作状态	开关状态				输出电平
工作状态	S_α1	S_α2	S_α3	S_α4	输出电平
P	1	1	0	0	V_dc/2
O	0	1	1	0	0
N	0	0	1	1	-V_dc/2
注：α =a, b, c

下载: 导出CSV

表 2 开关状态和共模电压之间的关系

矢量	开关状态	u_com
大矢量	[1 -1 -1] [-1 1 -1] [-1 -1 1]	-V_dc/6
大矢量	[1 1 -1] [-1 1 1] [1 -1 1]	V_dc/6
中矢量	[1 0 -1] [0 1 -1] [-1 1 0]	0
中矢量	[-1 0 1] [0 -1 1] [1 -1 0]	0
正小矢量	[0 -1 -1] [-1 0 -1] [-1 -1 0]	-V_dc/3
正小矢量	[1 1 0] [0 1 1] [1 0 1]	V_dc/3
负小矢量	[1 0 0] [0 1 0] [0 0 1]	V_dc/6
负小矢量	[0 0 -1] [-1 0 0] [0 -1 0]	-V_dc/6
零矢量	[-1 -1 -1][1 1 1]	-V_dc/2 V_dc/2
零矢量	[0 0 0]	0

下载: 导出CSV

表 3 主要参数

参数	数值	参数	数值
直流侧电压/V	500	参考电流频率/Hz	50
电容/μ F	3300	采样频率/kHz	10
负载电感/mH	5	λ₁	1.5
负载电阻/Ω	20	λ₂	0.5
参考电流/A	12	λ₃	0.5

下载: 导出CSV

表 4 运行时间对比

	运行时间/μ s	降低率（对比SVPWM）/%
SVPWM	19.78	-
MPC	13.26	33

下载: 导出CSV

参考文献(7)

[1]	Yuan Qingqing, Li An, Qian Jinyue, Xia Kun. Dc-link capacitor voltage control for the NPC three-level inverter with a newly MPC-based virtual vector modulation[J]. IET Power Electronics, Vol. 13, No. 5, pp. 1093-1102, 2020. doi: 10.1049/iet-pel.2019.0891
[2]	李宁, 王跃, 王兆安, 等. 一种三电平NPC变流器SVPWM策略的新型等效算法研究[J]. 电工电能新技术, 2015, 34(11): 11-17, 42.
[3]	林茂, 李颖晖, 李宁, 等. 三电平容错拓扑分析及预测控制研究[J]. 电力系统保护与控制, 2017, 45(1): 60-66.
[4]	Li Chen, Yang Tao, PonggornKulsangcharoen et al. A Modified Neutral Point Balancing Space Vector Modulation for Three-Level Neutral Point Clamped Converters in High-Speed Drives[J]. IEEE Transactions on Industrial Electronics, 2019, 66(2): 910-921. doi: 10.1109/TIE.2018.2835372
[5]	Jiang Dong, Shen Zewei, Wang Fei, "Common-Mode Voltage Reduction for Paralleled Inverters, " IEEE Transactions on Power Electronics, Vol. 33, No. 5, pp. 3961-3974, May. 2018.
[6]	Hou C C, Shih C C, Cheng P T, et al. "Commonmode voltage reduction pulsewidth modulation techniques for three-phase grid-connected converters, " IEEE Trans. Power Electron., Vol. 28, No. 4, pp. 1971-1979, Apr. 2013.
[7]	钱金跃, 吴佳, 施文杰, 等. 基于SVPWM的简化MPC算法的NPC三电平逆变器[J]. 浙江电力, 2022, 41(1): 80-88.

施引文献

资源附件(0)

图(5) / 表(4)

计量

文章访问数: 0
HTML全文浏览量: 0
PDF下载量: 0
被引次数: 0

1. NPC三电平逆变器
1.1 工作原理
1.2 数学模型
2. 中点电位不平衡及开关频率
2.1 不平衡分析
2.2 开关频率分析
2.3 共模电压分析
3. 模型预测控制
3.1 目标函数
3.2 控制策略
4. 仿真验证
5. 结束语

基于模型预测控制算法的NPC三电平逆变器

作者简介: 钱金跃(1994—), 男, 助理工程师, 逆变器控制研究

计量

出版历程